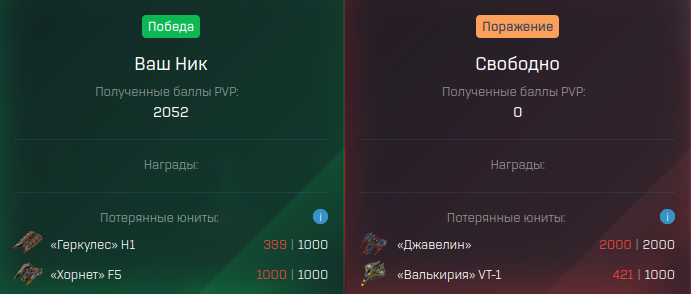
¶ Detailed analysis of Combat mathematics using examples
Surely, there are several ways to calculate. Also, for convenience, we will use an 80% accuracy roll everywhere. This means that all base damage of ships will be equal to 80% of the nominal damage.
¶ Example 1: Combat in space.
Fleet 1:
- 5000 Valkyries
- 100000 Javelins
- Level 40 Disintegrator module: +10% damage
Fleet 2:
- 33333 Raptors
- Shield Amplifier module level 100: +30% to Defense
Damage dealt by Fleet 1.
Valkyrie's nominal damage is 50 missile damage. From 80% accuracy we get 40 damage.
5,000 Valkyries will do 5,000 * 40 = 200,000 missile damage.
Javelin's nominal damage is 45 units of plasma damage. Accuracy will do 36 damage.
100,000 Javelins will deal 100,000 * 36 = 3,600,000 plasma damage.
The module will give us another +10%.
Total:
220,000 missile damage
3,960,000 plasma damage
Damage dealt by Fleet 2.
Raptor's nominal damage is 150 kinetic damage. With accuracy there will be 120 damage.
33,333 Raptors will deal 33,333 * 120 = 3,999,960 kinetic damage.
There is no damage module.
Total:
3,999,960 kinetic damage.
Superiority mechanic.
Note: below we use all defenses from each type of damage. In the current context, all of these defenses are 40%, 20% more or less than "average" defense (based on the type of damage the ship itself deals). Therefore, it would be possible to simplify the expression, since the sum of all defenses 0.6*x+0.8*x+x+1.2*x+1.4*x equals 5*x, where x - nominal or average protection. But if the game is rebalanced and defenses are untied from percentages, then we will have to use the sum of all defenses instead of the average defense multiplied by five.
So, first you need to calculate the total protection for each type of ship:
Valkyrie: 90+110+120+100+80 = 500
Javelin: 55+33+44+66+77 = 275
Raptor: 180+210+150+90+120 = 750
Then we calculate the total sum of defenses of Fleet 1 and 2:
Fleet 1: 5,000 Valkyrie * 500 + 100,000 Javelin * 275 = 30,000,000
Fleet 2: 33,333 Raptor * 750 = 24,999,750
Fleet 1 has more total defense, therefore the Superiority mechanic will affect it. The bonus itself is given for exceeding one amount over another.
Subtract the smaller from the larger: 30,000,000 - 24,999,750 = 5,000,250
And divide by the smaller: 5,000,250 / 24,999,750 = 0.200012
Constant: 12.5% bonus for every 100% exceedance.
Multiply 0.200012 by a constant in fractions of 0.125 = 0.0250015
This final bonus in fractions or 2.5% to defense will give Superiority.
Fleet's defense.
For Fleet 1, all nominal defense will be multiplied by 1.0250015 (from Superiority)
For Fleet 2, all nominal defense will be multiplied by 1.3 (from Module)
Receiving Damage by Fleet 2.
It only has one ship, so let's start with that. Let me remind you about the comparison of Defense with Health points in other games.
Raptor's final defense:
117 against missile damage
234 against plasma damage
Damage is dealt sequentially to each ship. Mathematically, this can be described as Subtracting incoming Damage from the Defense of all ships:
(33,333 * 234) defense against plasma - 3,960,000 plasma damage = 3,839,922 defense against plasma left.
Let's bring it back to the number of ships: 3,839,922 / 234 = 16,409.92 Raptors left.
Rounding occurs at the end of the battle.
Let's move on to the next damage:
(16,409.92 * 117) defense against missile - 220,000 missile damage = 1,699,961 defense against missile left.
Let's bring it back to the number of ships: 1,699,961 / 117 = 14529.58 Raptors left.
Now we can round. According to the mechanics of the game, if one ship has at least 50% health left, then it survives.
14,530 Raptors left after combat.
Receiving Damage by Fleet 1.
It will be more difficult here, since there are two ships here and there will also be excess damage that we will need to redistribute.
Let's start with Priorities, they will ultimately give us shares of damage to ships.
Valkyrie has Attack Priority 5,000, Javelin has 1,000.
Total Fleet Priority: 5,000 * 5,000 Valkyries + 1,000 * 100,000 Javelins = 125,000,000
Valkyries share: (5,000 * 5,000) / 125,000,000 = 0.2
Javelins share: (1,000 * 100,000) / 125,000,000 = 0.8
Actually, at the first iteration of Damage distribution, Valkyries will receive 20%, and Javelins 80% of incoming damage.
We can conclude that despite the difference in priorities (5,000 vs. 1,000), most of the damage went to Javelins due to their larger number.
Valkyries: 3,999,960 * 0.2 = 799,992 kinetic damage
Javelins: 3,999,960 * 0.8 = 3,199,968 kinetic damage
Final defense taking into account Superiority (2.5%).
Valkyries: 123.00018 from kinetics
Javelins: 45.100066 from kinetics
Damage to Valkyries:
Similarly to Raptors, we subtract Damage from Health:
(5,000 * 123.00018) - 799,992 = −184,991.1
This means that all Valkyries will be destroyed in the first iteration and the excess damage is equal to 184,991.1 kinetics. It will be redistributed further.
Damage to Javelins:
(100,000 * 45.100066) - 3,199,968 = 1,310,038.6 defense against kinetics left.
Let's bring it back to the number of ships: 1,310,038.6 / 45.100066 = 29,047.38 Javelins left.
Second iteration.
Damage to Javelins:
(29,047.38 * 45.100066) - 184,991.1 = 1,125,047.66 defense against kinetics left.
Let's bring it back to the number of ships: 1,125,047.66 / 45.100066 = 24,945.59 Javelins left.
24,946 Javelins left after combet.
Report.
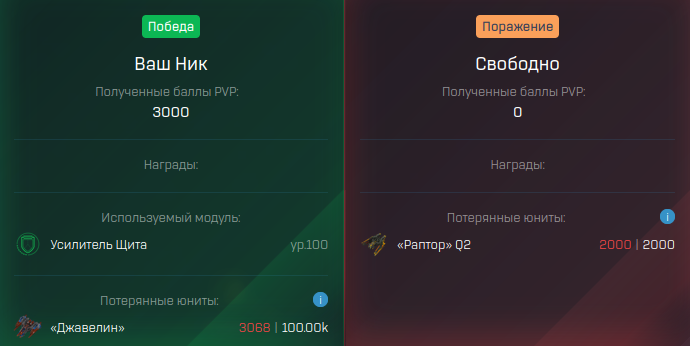
If in a real battle we had an accuracy roll of 80%, then in the report we would see (losses / total):
Fleet 1:
Javelin: 75.05k / 100.00k
Valkyrie: 5000 / 5000
Fleet 2:
Raptor: 18.80k / 33.33k
¶ Planet Blockade.
Here the battle between the attacking fleet and the existing Blockade will be similar to a battle in space, with the only difference being that the Blockade will use Defense Priority.
But in the Blockade it is still possible to launch Missiles, but we will consider it in Attack of the Planet.
¶ Example 2: Attack of the Planet.
Fleet 1:
- 100,000 Excaliburs
- 70,000 Abaddons
- Module +30% to Defense
Fleet 2:
- 10,000 Hornets
- Minterium planet with 5 mines: planetary coefficient is 3.6
- Rockets:
- 1,000 Cobra rockets
- 30,000 Aurora rockets
- Missile Towers:
- Sum of all levels 100 (for example, five Towers of level 20)
The first phase will be Rocket Launch.
Since there is no second fleet here, the Superiority mechanic naturally does not work.
Rockets have parameters: number of warheads and damage from one warhead. Their damage type is missile, regardless of type.
And the distribution of Damage occurs through the distribution of Rockets. If the ship has less defense than the warhead's damage, then it will deal damage equal to the defense and no more.
Priority is considered the same here, the values for existing ships are 1,000.
So, we calculate the share of each ship in the total number:
Excaliburs: 100,000 * 1,000 / (100,000 * 1,000 + 70,000 * 1,000) = 0.5882
Abaddons: 70,000 * 1,000 / (100,000 * 1,000 + 70,000 * 1,000) = 0.4117
A rocket is an indivisible entity, so the distribution of rockets necessarily involves rounding and checking the remainder. And also sequentially, because after the firing of some rockets, the number of the fleet will change.
Distribution. Cobras.
Cobra rockets per Excalibur:
1,000 * 0.5882 = 588.2 = 589
Here I don’t know exactly how rockets are rounded, but I always round up to the nearest whole number.
Cobra rockets per Abaddon: 1,000 - 589 = 411
This is the last ship, so we subtract everything that was used so that there is no “extra” rocket.
Protection of Excaliburs from missile damage is 275, and taking into account Module 357.5.
Abaddon's protection is 540, with Module 655.2
Cobras have 1 warhead, its damage is 150.
Damage to Excaliburs.
589 Cobra rockets = 589 * 1 warhead with 150 damage each = 88,350 missile damage
(100,000 * 357.5) - 88,350 = 35,661,650 defense against missiles left.
Let's bring it back to the number of ships: 35,661,650 / 357.5 = 99,752.87 Excaliburs left.
Damage to Abaddons.
411 * 150 = 61,650 missile damage
(70,000 * 655.2) - 61,650 = 45,802,350 defense against missiles left.
Let's bring it back to the number of ships: 45,802,350 / 655.2 = 69,905.91 Abaddons left.
Auroras.
We re-calculate the share of each ship in the total number:
Excaliburs: 99,752.87 / (99,752.87 + 69,905.91) = 0.587962
Abaddons: 69,905.91 / (99,752.87 + 69,905.91) = 0.412038
Aurora rockets per Excalibur: 30,000 * 0.587962 = 17,638.86 = 17,639
Aurora rockets per Abaddon: 30,000 - 17,639 = 12,361
Aurora has 4 warheads, the damage of one is 75.
Damage to Excaliburs.
17,639 Aurora rockets = 17,639 * 4 warheads with 75 damage each = 5,291,700 missile damage
(99,752.87 * 357.5) - 5,291,700 = 30,369,951.025 defense against missiles left.
Let's bring it back to the number of ships: 30,369,951.025 / 357.5 = 84,950.91 Excaliburs left.
Damage to Abaddons.
12,361 * 4 * 75 = 3,708,300 missile damage
(69,905.91 * 655.2) - 3,708,300 = 42,094,052.232 defense against missiles left.
Let's bring it back to the number of ships: 42,094,052.232 / 655.2 = 64,246.11 Abaddons left.
The second phase will be “passive” damage from Missile Towers.
The damage of one level of the Missile Tower is 100, then it is multiplied by the planetary coefficient. Minterium's coef with 5 mines is 3.6. We get 100 * 3.6 = 360 damage.
The Missile Tower's damage varies linearly with the level of the building. Thus, the total damage of all Missile Towers on a given planet will be equal to:
360 * 100 levels = 36,000 railgun damage (Towers do this type of damage)
Distribution is still the same, 1,000 is the priority value for ships:
Excaliburs: 84,950.91 * 1,000 / (84,950.91 * 1,000 + 64,246.11 * 1,000) = 0.5694
Abaddons: 64,246.11 * 1,000 / (84,950.91 * 1,000 + 64,246.11 * 1,000) = 0.4306
Protection of excaliburs from railgun is 165, and taking into account Module 214.5.
Abaddon protection is 360, with Module 468
Damage to Excaliburs.
(84,950.91 * 214.5) - 36,000 * 0.5694 = 18,201,471.795 defense left
Let's bring it back to the number of ships: 18,201,471.795 / 214.5 = 84,855.35 Excaliburs left.
Damage to Abaddons.
(64,246.11 * 468) - 36,000 * 0.4306 = 30,051,677.88 defense left
Let's bring it back to the number of ships: 30,051,677.88 / 468 = 64,212.99 Abaddons left.
The third phase will be the battle with the fleet on the planet.
Damage dealt by Fleet 1.
Excaliburs: 84,855.35 * 225 * 0.8 (accuracy) = 15,273,963 missile damage
Abaddons: 64,212.99 * 440 * 0.8 = 22,602,972.48 railgun damage
Damage dealt by Fleet 2.
Hornets: 10,000 * 110 * 0.8 = 880,000 laser damage
Superiority.
We will not repeat the calculations, because here the naked eye can see that Fleet 1 is quite superior to Fleet 2. There will be a maximum bonus of 50%.
Damage distribution.
Excaliburs: 84,855.35 * 1,000 / (84,855.35 * 1,000 + 64,212.99 * 1,000) = 0.5692
Abaddons: 64,212.99 * 1,000 / (84,855.35 * 1,000 + 64,212.99 * 1,000) = 0.4308
Excalibur's defense against laser is 330, bonuses from Module and Superiority stack, 594
Abaddon's defense is 288, with bonuses 518.4
Hornet's defense against missile is 72, against railgun is 108
Fleet 1 receives Damage.
(84,855.35 * 594) - 880,000 * 0.5692 = 49,903,181.9 defense left
Let's bring it back to the number of ships: 49,903,181.9 / 594 = 84,012.09 Excaliburs left.
(64,212.99 * 518.4) - 880,000 * 0.4308 = 32,908,910.016 defense left
Let's bring it back to the number of ships: 32,908,910.016 / 518.4 = 63,481.69 Abaddons left.
As a result, after the battle 84,012 Excaliburs and 63,482 Abaddons survived.
Fleet 2 receives Damage.
Missile damage.
(10,000 * 108) - 15,273,963 = −14,193,963
This means that all Hornets have been destroyed and that 14,193,963 missile damage remains. Let me remind you that if there had been another type of ship in the defense and they had not been destroyed during the first iteration, then this damage would have been distributed further.
Report.
If in a real battle we had an accuracy roll of 80%, then in the report we would see (losses / total):
Fleet 1:
Excalibur: 15.99k / 100.00k
Abaddon: 6.52k / 70.00k
Fleet 2:
Hornet: 10.00k / 10.00k
¶ Ship parameters

¶ Rocket parameters

¶ Additional examples
I invite the reader to make several calculations to choose from.
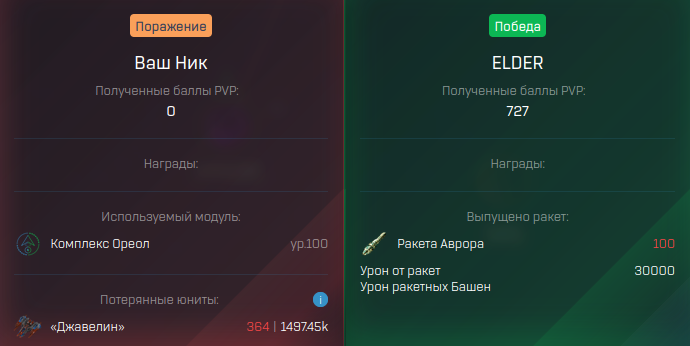
¶ Example 1
Javelins in the Blockade on the Quest, Halo module, +25% to defense.
¶ Example 2
Attack of the Planet Torium with 3 mines, planetary coefficient is 0.8;
one Missile Tower of the first level, 100 Cobra rockets (1 warhead with 150 damage)
Note: Warhead damage will not exceed the ship's defense.
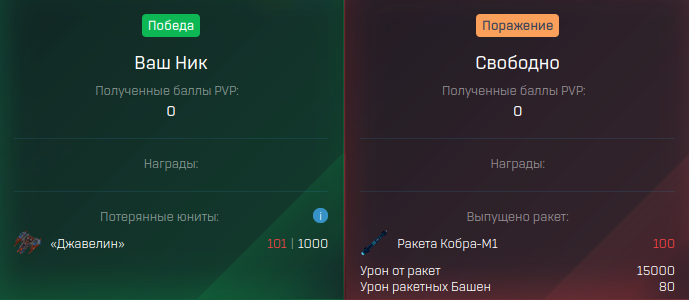
¶ Example 3
Attack of the Planet Torium with 3 mines, planetary coefficient is 0.8;
one Missile Tower of the first level, 100 Cobra rockets (1 warhead with 150 damage), 300 Aurora rockets (4 warheads with 75 damage);
Shield Booster module, +30% to defense.
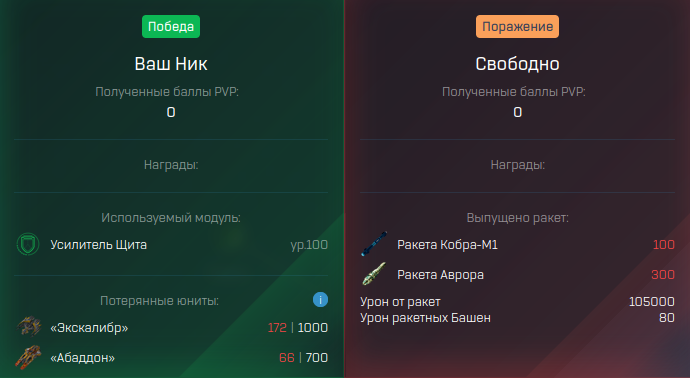
¶ Example 4
Attack of the Planet without rockets and towers;
Shield Booster module, +30% to defense.
There is an accuracy roll, I suggest counting two options: 80% accuracy and 100%. And compare the report with the boundaries: result 80% <= report <= result 100%.
Note: all bonuses are cumulative.
¶ Example 5
Attack of the Planet without rockets and towers;
There is an accuracy roll, I suggest counting two options: 80% accuracy and 100%. And compare the report with the boundaries: result 80% <= report <= result 100%.
Note: the impact of Priority and attack type on damage distribution.